手机版
一般来说，物体在某一段时间内运动的快慢通常是变化的。所以由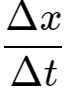 
求得的速度v，表示的只是物体在时间 Δt 内运动的平均快慢程度，叫作平均速度（average velocity）。
比如，百米赛跑的运动员在整个比赛过程中的快慢肯定是不一样的，假设他用10s跑完全程，那么速度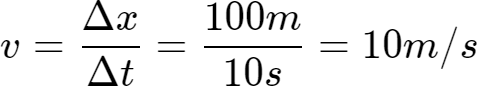
，很显然这个速度不能准确的描述运动员在比赛过程中的快慢，只能表示这个过程中的平均快慢程度，所以叫做平均速度，通常用
表示（这里注意一下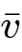
的上面是一条短横线，而向量的上面是一个箭头）。
看一下课本上的思考题
截取自人教版《高中物理》
速度是一段时间内位移与时间的比值，而现在要描述的是某一时刻运动的快慢，那么速度的定义还适用吗？
平均速度只能粗略的描述物体在某段时间内的平均快慢程度。那么为了更加精确的描述物体的运动，可以设想用由时间t 到t ＋Δt 这一小段时间内的平均速度来代替时刻t 物体的速度。如果Δt 取得小一些，物体在Δt这样一个较小的时间内，运动快慢的差异就不会太大。Δt 越小，运动快慢的差异就越小。当 Δt 非常非常小，即无限的趋近于0时，运动快慢的差异可以忽略不计，此时我们就把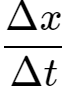
叫作物体在时刻 t 的瞬时速度（instantaneous velocity），写成
。
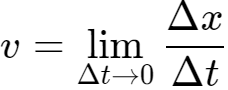所以瞬时速度可以认为是质点在某时刻前后极微小时间间隔内，或某位置附近极微小位移内的平均速度。
当物体做匀速直线运动的时候，任何时刻的瞬时速度都保持不变。也就意味着在整个运动过程中，任何一段时间内的平均速度与任何一时刻的瞬时速度都相等。
当物体做变速直线运动时，每个时刻的运动情况可能都不同，因此质点的瞬时速度都不相等。
如果要求平均速度，必须要指明是在哪一段时间内，或者哪一段位移上平均速度。在不同时间内或者不同位移上的平均速度一般不同。
在题目中，速度一词有时指平均速度，有时指瞬时速度，需要结合上下文内容仔细判断。比如，一辆汽车从静止加速到40m/s的速度需要10s，总共前进了200m。40m/s是汽车在第10s末达到的速度，就是瞬时速度；在整个10s的加速时间内，平均速度大小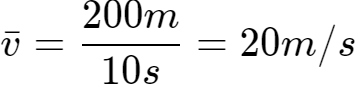
。
而汽车仪表盘上的读数通常指的是瞬时速度，比如 60 km/h。
汽车仪表盘
平均速度和瞬时速度都是矢量，满足矢量的特点，既有大小又有方向。平均速度的方向是对应时间内位移的方向；瞬时速度的方向与物体经过该位置时的运动方向相同；如果是曲线运动，瞬时速度的方向就是轨迹上每点的切线方向。
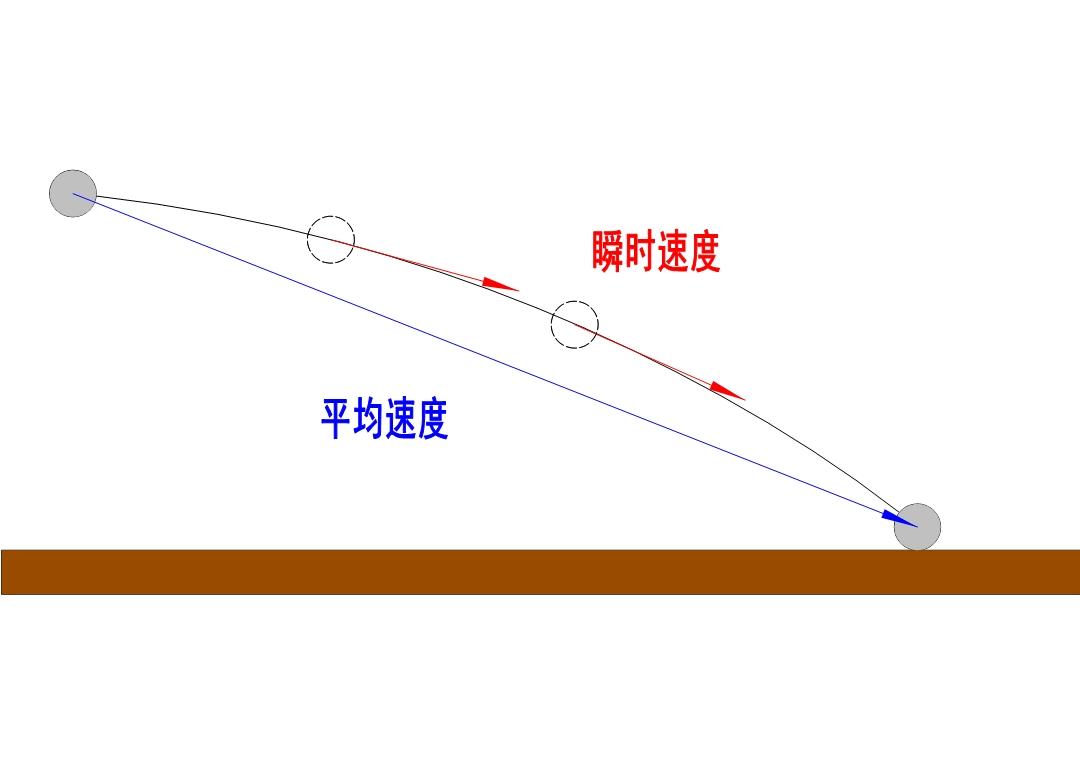
如上图，将一个小球从空中抛出直到落至地面，整个过程的平均速度方向由初位置指向末位置；但在空中任意位置的瞬时速度方向就是该点切线的方向。
总结
平均速度：粗略描述质点在一段时间内或一段位移上的运动快慢。
瞬时速度：精确描述质点在某一时刻或某一位置的运动快慢。
平均速度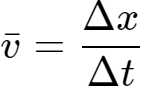
，当Δt→0时，平均速度就是瞬时速度，即
。
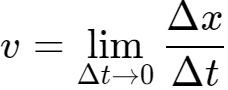平均速度和瞬时速度都是矢量。
