直线的参数方程怎么求（一题多解，参数方程极坐标全用到）

本文原创例题

【解前分析】

题目虽不复杂，

但要控制好解题导向，

就有点难度；

计算粗心、寄希望于做完后再检查的同学，

请注意一遍算对。

我提供四种解法。

建议您看完题后，

自己做一下，再对照，不宜直接阅读。

解法一：

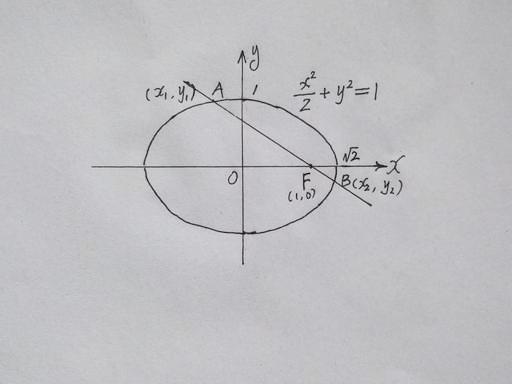
由题意，

椭圆的右焦点坐标为

F(1，0)，

故设直线L的方程为

y=k(x-1)，

直线方程与椭圆方程

联立，方程组的解即为

两个交点的坐标。

把y=k(x-1)代入

椭圆方程得：

正在求k值，接下图。

解法一完毕。

解法一的计算量有点大，

只要在演算之上一步一步地写，

别脑算跳步骤，一般不会出错。

如果喜欢脑算加心算，

总是一家伙写出几步之后的算式，

保证一张卷子还没做完就头昏脑胀了。

请谨记：一步一步地写！不费脑筋！

保持整个考试过程头脑清醒！

从不要想一口吃胖！

解法二。

下同解法一。

分析角度不同，

则解题导向亦不同。

解法二的计算量明显很小。

解法三：参数方程法。

我们知道：

过点M0(X0，Y0)且

倾斜角为θ的直线的

参数方程为：

X=X0+tcosθ

Y=Y0+tsinθ

其中θ应满足[0，π)，

参数t的绝对值表示

它对应的点到定点M0的距离。

∵点A在点B上方，

∴y1＞0＞y2，

由于|AF|/|BF|=4，

∴点A对应的参数t＞0，

点B对应的参数(-t/4)＜0。

直线L经过点(1，0)，

故设直线L的参数方程为：

x=1+tcosθ

y=0+tsinθ

t为参数，

θ为直线L的倾斜角。

A、B两点在椭圆上，故：

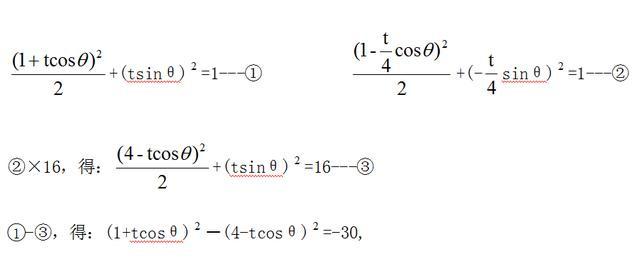
解法三，参数方程法，接下图。

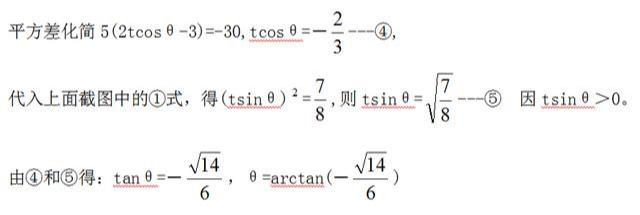
解法三参数方程法，接下图。

解法三完毕。

解法四：极坐标法。

圆锥曲线中，

离心率e=c/a,

焦点到准线的距离

p=b平方/c。

本题中，

a=根号2，c=1。

圆锥曲线统一极坐标方程为

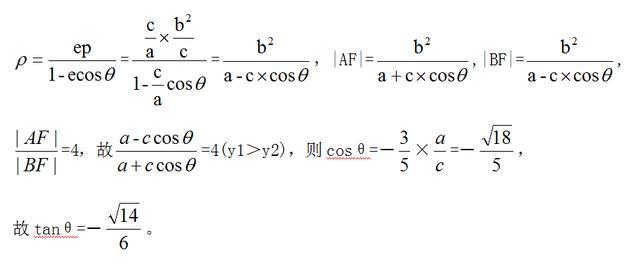
解法四，简洁吧？

【解后反思】

以上四种解法，由繁到简，

请注意知识的综合运用。

仔细审题，

如果忽略y1＞y2，

则导致不必要的分类讨论。